If you have been in a computer science class, then most probably you have covered a unit called "Data Structures & Algorithms". The name might be some what different but, yeah, you get the idea. If you haven't, then I'll try to make it as understandable as I possibly can.

Algorithms, in brief, are just a finite number of steps towards achieving a particular task, at least in the most layman of explanations. Think of going to work for instance. You have to:

1. Wake up
2. Brush your teeth
3. Take a shower (or bath)
4. Choose & wear the right attire
5. Leave the house (unless you're working from home)

(Your morning routine might be different from mine, but, you get the point.. )

Solving a computing task is somewhat similar, only that in this case, you are telling the computer what to do. In this article we'll look at an example of an algorithm called the Insertion Sort algorithm.

---

In a nutshell...

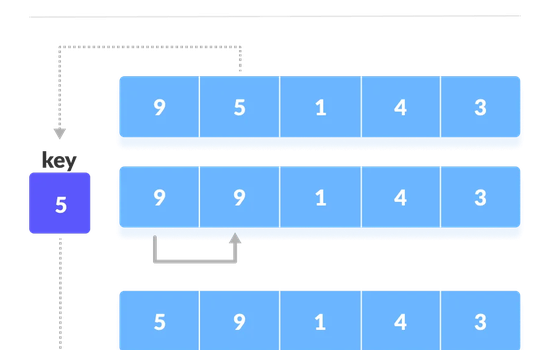
Insertion Sort works by iterating over a list of elements and placing the unsorted items in their right or suitable "slot" by pushing the other elements to the right/left depending on the order of sorting.

Think of sorting a pile of cards placed face down on a table, by hand.

You pick the first card, then the second, check if the number on the second card is greater or less than the first card, then place it either above or below the first card depending on the order, then repeat the same procedure for the 3rd, 4th,...nth card on the pile of cards where n is the total number of cards on the pile.

So ideally the algorithm for this sorting task would look something like:

1. loop from the second element of the list to the last
2. key = current element in loop
3. compare key with left element(s):
4. while index of left element is greater than 0 and left element is greater than key:
5. push left element to the right
6. go to the next left element (if any)
7. Repeat until we exit the loop
8. place key next to the smallest element
9. return sorted list

Next, well write some Pseudocode to make it more code-familiar :-) (Okay, this is the part where most people start getting scared... Don't be)

for i = 2 to Array.length
    key = Array[i]
    adj_index = i - 1

    while adj_index > 0 and Array[adj_index] > key
        Array[adj_index + 1] = Array[adj_index]
        adj_index = adj_index - 1
    
    Array[adj_index + 1] = key

So what exactly is going on here?

We begin by iterating the array from the second element to the last, while assigning the current element as the key and taking note of the adjacent element's index (line 1-3).

We then check if the adjacent element is greater than the key and if it is, we push that element to the right (line 6), then go to the next left/adjacent element (line 7) and check for the same condition. We repeat this until we reach the first element in the list, i.e, index 0 (loop applies for lines 5, 6 and 7).

Once we exit the loop, we insert the key next to the smallest element in the list (line 9)

We then repeat this for all the items in the list.

So ideally, we have two loops in our algorithm. One to iterate over all the elements in the array (the pile of cards on the table), and another to iterate over all elements from the start of the array to our current key (the cards on the hand).

I hope the above illustration gives you a vivid image of how this works. If not, do not despair. Go through the last few paragraphs again, slowly by slowly (it actually works :).

---

Code Example

For all illustrations in my projects and articles, I use the Python programming language, as that is what I use on a daily basis (at least for now), but it should be easy to follow and adapt to your syntax/language of choice. So here follows the code to perform an insertion sort, given an array.

def sort_by_insertion(array):
    for i in range (1, len(array)):
        key = array[i]
        step = i-1 # Denotes the next left element

        while step >= 0 and array[step] > key:
            array[step+1] = array[step]
            step -= 1

        # Loop above will exit if either:
        # 1. step index is less than 0
        # 2. key exceeds element at current step index

        # Insert key in the next smallest index after the loop
        array[step+1] = key

    return array

array_to_sort = [31, 41, 59, 26, 41, 58]
print(sort_by_insertion(array_to_sort))

The code should be easy to read especially if you understood the pseudocode above. I hope this gives you some insights into how insertion sort works both from a literal and technical points of view.

I'll be writing more about the analysis of the insertion sort algorithm in a future article. Meanwhile if you liked this article, or have some feedback/thoughts on it, simply let me know.

Cheers!